Función de R: block average

Comúnmente en nuestros estudios, necesitamos el valor medio de una secuencia de números, así también como un nivel de incerteza para esa estimación. Esto es, el error estándar, el cual se calcula como el cociente entre la desviación estandar de los datos y la raíz cuadrada del número de observaciones.

Sin embargo, este procedimiento resulta erróneo cuando nuestros datos no son independientes. Este es el caso, por ejemplo, de las series temporales: cada nuevo valor de la serie depende en mayor o menor medida de los valores registrados anteriormente.

El método “block average”

Calcular el error estándar de datos no independientes mediante la fórmula clásica arrojará un valor artificialmente pequeño. Aún tengamos n muestras, estas no son independientes (por ejemplo, en el caso de series temporales), por lo que en realidad tendremos un menor número de muestras independientes. El método “block average” (no encontré referencias de este método en español) es útil para tratar este problema. El mismo consiste en dividir los datos (N valores) en n bloques de igual tamaño s (n * s = N). Luego, calculamos el valor medio para cada bloque, la media de estas medias por bloque, y el error estándar para esta última (la media de medias).

La clave del método consiste en determinar el tamaño “correcto” de los bloques, a partir de los cuales los bloques de datos son independientes entre sí. Una buena forma de hacer esto consiste en calcular el error estándar para la media de las medias (en plural, por cada media calculada por bloque de un tamaño determinado), para diferentes tamaños de bloques. Luego, se grafican estas estimaciones en función de los tamaños de los bloques. El mejor valor para el error estándar será aquel que se mantiene más o menos constante a medida que el tamaño de los bloques crece.

Para este propósito, he programado una función en R. Veamos un ejemplo que creo esclarecerá el método.

En primer lugar, simulemos algunos datos alreatorios y no independientes. Una serie temporal:

# Fijamos la semilla para obtener siempre los mismos resultados
set.seed(42)

# Generamos 1000 valores aleatorios a partir de una distribución normal
# con media = 1 y desviación estandar = 10
x <- rnorm(1000, mean = 1, sd = 10)

# Generamos una nueva variable "sum" la cual será calculada como la suma
# del valor en cada momento, más los últimos tres valores premultiplicados
# algún coeficiente aleatorio
sum <- rep(0, length(x))
sum[1] <- x[1]
for(i in 2:length(x))
{
  # Hacer el cálculo sólo si hay 3 valores previos
  if(i > 3)
  {
    sum[i] <- runif(1, 0.5, 1) * x[i] + runif(1, 0.4, 0.6) * sum[i-1] + 
              runif(1, 0.2, 0.4) * sum[i-2] + runif(1, 0, 0.2) * sum[i-3]
  }
  else
  {
    sum[i] <- sum[i-1] + x[i]
  }
}

Veamos como se ve esta serie temporal en un gráfico:

Serie temporal simulada

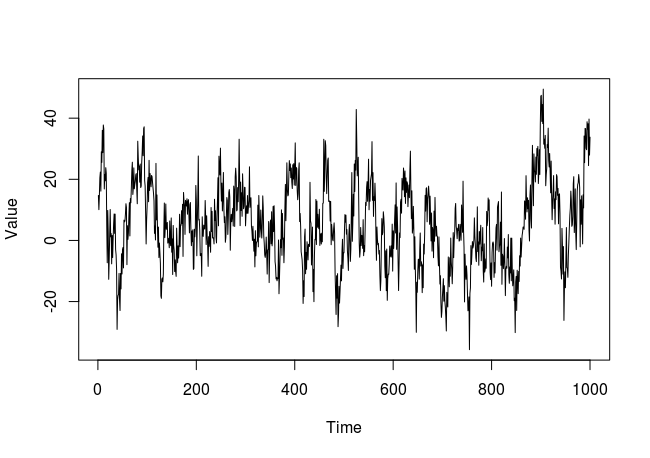
Apliquemos el método “block average”, usando la función block_average en R. Esta función tiene tres argumentos: x es la secuencia de números (un vector numérico) a partir de la cual queremos calcular un error estándar; block_sizes es un vector numérico que contiene los diferentes tamaños de bloque a evaluar; y n_blocks es un vector numérico con el número de bloques a evaluar. Los dos últimos argumentos son opcionales, aunque se recomienda definir uno de ellos. Si se define n_blocks, los tamaños de los bloques a evaluar se calculan automáticamente. Por ejemplo, imaginemos que tenemos una secuencia de 100 números de una serie temporal y definimos n_blocks = c (10, 25, 50). Luego, los tamaños de los bloques se calcularán haciendo el cociente entre 100 (la longitud de la secuencia numérica) y cada número definido en n_blocks: 10, 4 y 2. Si ambos argumentos están definidos, la función solo trabaja con los valores definidos en block_sizes. Recomiendo definir manualmente los tamaños de bloque en el argumento block_sizes, ya que es más intuitivo.

La función genera un gráfico de puntos con los errores estándar en relación con el tamaño del bloque. Si se asigna a un objeto, la función también devuelve un data.frame a partir del cual se creó el gráfico. Esto puede resultar útil si el usuario desea realizar análisis adicionales. En nuestro ejemplo:

# seq(5, 150, 5) define una secuencia de números desde 5 a 150, cada 5
block_average(x = sum, block_sizes = seq(5, 150, 5))

El gráfico:

Errores estándar a diferentes tamaños de bloques. Serie temporal.

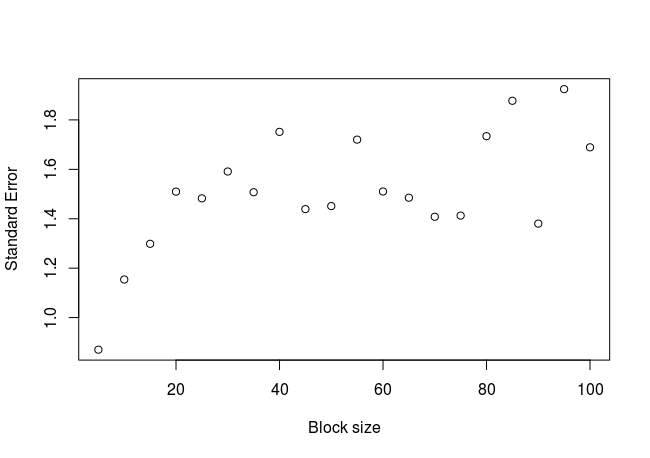
Podemos ver que el error estándar aumenta de forma aparentemente logarítmica, hasta un valor de aproximadamente 1,6 a partir del cual la tendencia parece estabilizarse. Podríamos ajustar una curva a esta nube de puntos, para obtener un valor más preciso del error estándar una vez estabilizado (no se hace aquí). ¿Qué pasa si calculamos el error estándar de la forma clásica?

sd(sum) / sqrt(length(sum))
>> 0.4302361

Como era de esperar, el error estándar calculado con el método “block average” es mayor que el calculado clásicamente. Esto sucede porque el número de muestras independientes reales es menor que el número total de muestras.

¿Qué sucede si aplicamos el método “block average” a un conjunto independiente de números? En la secuencia simulada anterior, el vector x contiene números aleatorios e independientes. Apliquemos la función a este vector:

block_average(x = x, block_sizes = seq(5, 150, 5))

El gráfico:

Errores estándar a diferentes tamaños de bloques. Datos independientes.

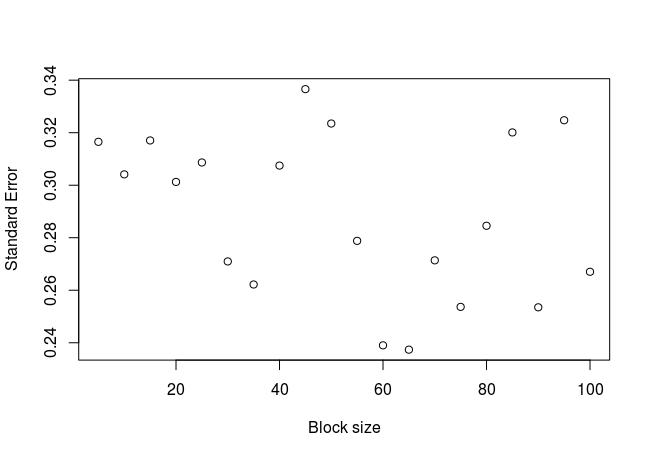
Como era de esperar, cuando los datos son independientes, no existe una relación clara entre el error estándar y el tamaño del bloque.

Aquí hay algunas referencias del método:

http://sachinashanbhag.blogspot.com/2013/08/block-averaging-estimating-uncertainty.html

https://www.quora.com/What-is-the-block-average-method

http://realerthinks.com/block-averaging-bootstrapping-estimating-mean-autocorrelated-data/

El código está disponible en my página de GitHub, aquí.